Theoretical Foundations of Deep Learning: TUM als stärkste Institution
Die Projekte der TUM befassen sich mit dem impliziten Bias von DL-Algorithmen, der Analyse von DL mittels dynamischer Systeme, der Robustheit von Graph Neural Networks, dem Lösen inverser Probleme mittels DL und den statistischen Grundlagen von un- und semi-überwachtem DL. Weitere Informationen finden Sie auf den Webseiten des Programms oder der DFG. Die TUM ist an den folgenden Projekten beteiligt.
Principal Investigator: Debarghya Ghoshdastidar
Researcher: Pascal Esser
Abstract: Recent theoretical research on deep learning primarily focuses on the supervised learning problem, that is, learning a model using labelled data and predicting on unseen data. However, deep learning has gained popularity in learning from unlabelled data or partially labelled data. This project provides a mathematically rigorous explanation for why and when neural networks can successfully extract information from unlabelled data. The project specifically provides statistical performance guarantees for semi-supervised learning using graph neural networks, and for unsupervised representation learning and clustering using autoencoders.
Implicit Bias and Low Complexity Networks (iLOCO)
Principal Investigators: Massimo Fornasier & Holger Rauhut (RWTH Aachen)
Abstract: In this project, we aim at contributing to the theoretical foundations of the implicit bias of gradient descent and its stochastic variants for training deep nonlinear networks and the relationship with low complexity networks. We shall leverage the intrinsic low complexity of trained nonlinear networks to design novel algorithms for their compression. As a byproduct we will show robust and unique identification of generic deep networks from minimal number of input-output samples. Besides advancing on the theoretical level, the project will develop new algorithms and software of practical relevance for machine learning, solution of inverse problems and compression of neural networks for their use on mobile devices.
Principal Investigator: Stephan Günnemann
Researcher: Jan Schuchardt
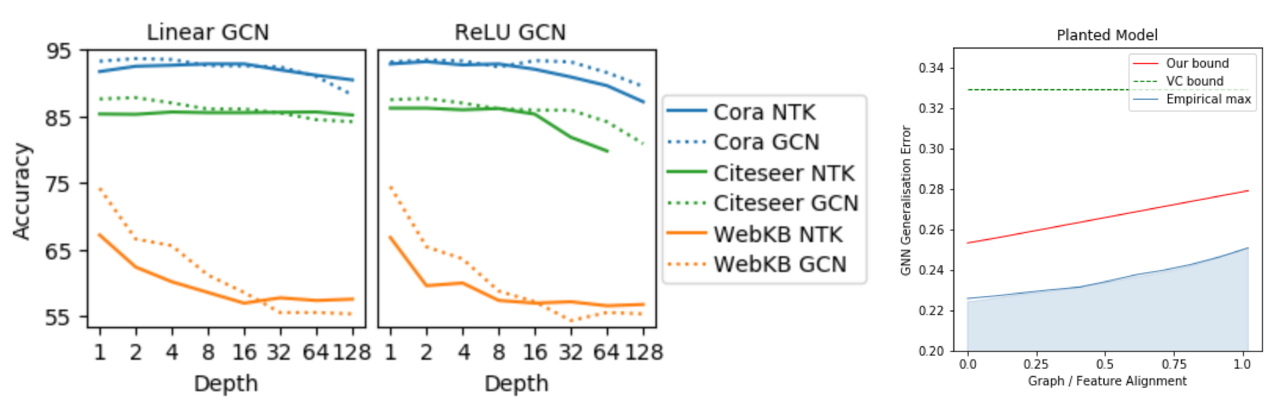
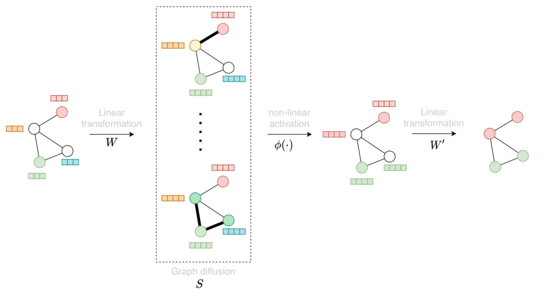
Abstract: Graph Neural Networks (GNNs) have become a fundamental building block in many deep learning models, with ever stronger impact on domains such as chemistry, social sciences, biomedicine, and many more. Recent studies, however, have shown that GNNs are highly non-robust. This is a show-stopper for their application in real-world environments, where data is often corrupted, noisy, or sometimes even manipulated by adversaries. The goal of this project is to increase trust in GNNs by deriving principles for their robustness certification.
Principal Investigators: Reinhard Heckel & Felix Krahmer
Abstract: Deep neural networks have emerged as highly successful and universal tools for image recovery and restoration. While the resulting networks perform very well empirically, a range of important theoretical questions are wide open. The overarching goal of this project is to establish theory for learning to solve linear inverse problems with end-to-end neural networks.
Principal Investigators: Christian Kühn & Maximilian Engel (FU Berlin)
Researcher: Dennis Chemnitz (FU Berlin)
Abstract: In the proposed research project, we aim at combining several recently developed mathematical approaches from dynamical systems theory to provide a new rigorous framework for machine learning in the context of deep neural networks. We will analyze deep neural networks by identifying two different dynamical time scales which are then combined in a stochastic multiscale dynamical system.